|
 |
Home ⇒ golf ⇒ design ⇒ Current Article |  |
Article
Contents
|
|
| e = | An efficiency measure of momentum
transfer called the Coefficient of Restitution (COR). Typical values
are:
|
| m = | Mass of the ball (typically 46 grams or 1.62 ounces). |
| M = | Mass of the clubhead (typically 200 grams or 7 ounces for driver). |
- A 10% increase in clubhead speed with no change in clubhead weight increases ball velocity 10%.
- A 10% increase in clubhead weight with no change in clubhead speed increases ball velocity only 1.7%.
This formula assumes a low-loft club like a driver. The higher the loft, the more the "leakage" of ball speed, as more of the energy of impact goes into producing spin instead of speed.
It's interesting to look at some of the things people think are important to distance (gauged from recent posts in rec.sport.golf), and compare them with facts:
- Square clubface and direction of clubhead travel: Right on! The equation assumes that the clubface is square to the direction it is traveling. If not (due to improper swing or a lofted clubface), a lot of the momentum will be transferred to sidewise motion and spin, instead of ball speed.
- Center impact on the clubface:
Right on! Every club has a "sweet spot" somewhere near the middle of
the face. The equation above assumes you hit the sweet spot. If you
miss it, you lose ball speed. I have seen estimates as high as 7% loss
of distance for every half inch you miss the sweet spot.
- Strength or weight of the golfer holding the club: Simply not a factor! If the golfer couldn't convert strength and weight into clubhead speed, then there's nothing that they can do during impact to increase distance. As we saw in the section on vibrational frequency, the clubhead is swinging free at this point, with little more connection to the grip than if it were on a string.
Actually, that's an overstatement. The shaft is infinitesimally stiffer than a string. If you do something at the grip during impact, 1/10,000 of that effect will reach the clubhead while the ball is still there. But that's all.
- Distance is a strong function of clubhead speed.
- Distance is a weak function of clubhead weight.
- If you can't swing a heavier clubhead very nearly as fast as a lighter one, the heavier head will cost you distance.
- If
you can't bring the clubhead into the ball with good impact (center of
clubface, with clubface square to the path of the clubhead), you will
lose more distance than you might imagine.
Loft and Spin
The information here is qualitatively well known. But recently, I've been able to do a little quantification as well, using a computer program written by Max Dupilka.Here are a few surprising facts about how loft affects distance:
- Air, while presenting drag to slow the ball, also presents lift to a ball with backspin. This keeps it in the air longer, and lets it go much further. A ball struck by a driver in a vacuum will travel less than 2/3 the distance it will in normal earth atmosphere.
- In seeming contradiction, drives go further at altitude where the air is thinner. It really isn't a contradiction, though; as air gets thinner, distance peaks at about 90% of the density at sea level, and drops off pretty sharply at less than 80% of the sea level density. The distance peak is only a few percent better than sea level.
- The more clubhead speed you generate, the lower you want your driver loft (down to some reasonable minimum). Conversely, the less your clubhead speed, the more loft you want on your driver. Now that I've run some curves on Max's program, I have a better feel for what's going on here.
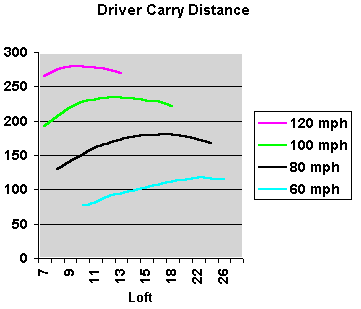First the curves, which show
carry distance (no roll) vs
loft,
for several clubhead speeds. Note that the higher the clubhead speed,
the lower the loft that achieves maximum carry. - For a 120mph clubhead, the maximum carry occurs at 10 degrees of loft.
- For a 80mph clubhead, the maximum carry occurs at 16 degrees.
The reason is that ball speed "amplifies" the lifting effect. Moreover, a higher clubhead speed puts more spin on the ball to produce lift. Between the two, a high clubhead speed can use lift to keep the ball in the air; it doesn't need as much loft.
Before you dive right in and use these numbers directly for clubfitting, let me remind you that:
- They are for carry only, and don't include roll.
- They don't include shaft flex, which changes the effective loft at impact.
Golf is Not Artillery
Let me end this section by dispelling a common myth, based on a misinterpretation of a well-known "law" of physics. As many of us learned in Physics 101, an object travels furthest if launched at an angle of 45 degrees. Why does this not seem to apply to the design of golf clubs? We all know that a 45º loft is about that of a pitching wedge, and a 45º launch angle requires considerably more loft than that. From experience, we all know that clubs with that much loft don't hit the ball nearly as far as the lower-lofted clubs.
Here is what's happening:
The Physics 101 problem assumed that
the ball starts at the same speed,
no matter what
the angle of takeoff. This is a true assumption for artillery, which is
where the problem originated. In artillery, you change the launch angle
by tilting the cannon up or down, which doesn't hurt the "ball speed"
at all.
But, for the golf model, increasing the launch angle usually
involves increasing the loft. As noted above, this causes ball-speed
"leakage", as more of the impact energy is turned into spin instead of
ball speed. By the time you get to a 45º launch angle, you are
hitting a very high-lofted wedge with lots of height and rather little
distance.
In order to duplicate the "artillery model" with a golf swing, it would require you to cause the 45º launch by using a tee more than a foot tall, and hit the ball with a low-loft driver on a 45º upswing.
I hope that made sense.
|
|
|